概念文字

《概念文字》（德语：Begriffsschrift）是1879年出版的戈特洛布·弗雷格写的一本关于逻辑学的书。书的完整标题把它标识为《模仿算术的纯思维的形式语言》。这本小书无可争议是亚里士多德之后在逻辑学领域最重要的出版物。弗雷格开发他的形式逻辑系统的动机是类似于莱布尼兹对“演算推论器”的渴望。

弗雷格定义了逻辑演算来支持他在数学基础上的研究。“概念文字”是书和其中定义的演算二者的名字。

演算介入了量词，因而本质上是经典的谓词逻辑，尽管使用了一种特异的二维记号（notation）：连结词和量词使用连接公式的线条来书写，而不是今天使用的符号（symbol）¬、∧、∀。例如，在判断B和A之间的蕴涵，也就是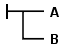${\displaystyle B\to <!--\; \to \; -->A}$用来指定。

在他的著作的第一章中，弗雷格确定了基本概念和标号（sign），象命题（"断定／判断"），和全称量词（"普遍性"），蕴涵（"条件性"），否定和等号${\displaystyle \equiv <!--\; \equiv \; -->}$；在第二章中他声明了九个形式化的命题作为公理（它们是在语义上证明了的形式化陈述）。

${\displaystyle p(A)=i}$

${\displaystyle B\subset <!--\; \subset \; -->A}$

他给出了条件的定义（第1章。§5.）:

设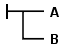标示（sign）第三种可能性是不能得到的，而只能是其他三种中的一个。所以如果我们否定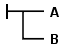就意味着第三种可能性是有效的，就是说我们否定了A并肯定了B。"

弗雷格声明了九个重言式断定作为公理。他以语义方式证明了它们，并以语法上的演绎证明了其他重言式断定。

弗雷格在第二章中历数了被形式化的命题；成为了他的公理的是第1st, 2nd, 8th, 28th, 31st, 41st, 52nd, 54th, 58th个命题。

他在这章中还声明了两个推理规则：它们是肯定前件；和代换律。在第一章中他宣布了一个约定，即“普遍化律”。这意味着如果“自由变量”能在一个断定中找到，则把它当作全称量化的，依据弗雷格的定律，在${\displaystyle ⊢<!--\; ⊢\; -->}$标号（“断定符号”）之后的，被固定的（fixed）变量是断定，而不是“开放”的公式，也就是谓词。

弗雷格在第二和第三章中在语法上证明了一百多个形式陈述。第三章（"Parts from a general series theory"）是对他在建造算术上做的工作的介绍。

它的记号的某些痕迹幸存了：被逻辑学家非正式的叫做“十字转门”（turnstile）的符号${\displaystyle ⊢<!--\; ⊢\; -->}$演化自弗雷格的“Inhaltsstrich”─和“Urteilsstrich”│。弗雷格在《概念文字》中以合一的形式├─使用这些符号来声明一个命题是（重言式）真的，而不是简单的宣布它。他使用“Definitionsdoppelstrich”│├─作为表示一个命题是一个定义的符号。

在逻辑哲学论中，维特根斯坦通过使用术语“概念文字”作为逻辑形式主义的同义词来表达对弗雷格的敬意。

在弗雷格后来的著作《意义和引用》中，它放弃了在本书中关于同一性达成的某些结论（用数学上的 = 号来标记）。

"如果哲学的任务是打破言辞在表达人类思想上的统治，那么我的概念记号，就是为这个目的而开发的，它能够成为哲学家的有用的工具我认为，只是通过发明这些概念记号，逻辑的本质（matter）就已经被促进了（forward）。"