牛顿环

在光学中，牛顿环（Newton's rings），也叫做牛顿圈，是一个等厚薄膜干涉现象。将一块平凸透镜凸面朝下放在一块平面透镜上，将单色光直射向凸镜的平面，可以观察到一个个明暗相间的圆环条纹。若使用白光，则可以观察到彩虹状的圆环彩色条纹。第一个对此现象进行分析的人是英国物理学家艾萨克·牛顿爵士，因而命名为牛顿环。

牛顿环现象是由平凸透镜下凸面和平面透镜的上平面（即两透镜间的空气薄膜的上下表面）所分别反射的光线产生干涉的结果。光线进入平凸透镜到达凸面进入空气时，一部分在该界面发生反射，另一部分透射后在下方的平面透镜发生反射，并与前一束后一次反射是在空气（光疏介质）—玻璃（光密介质）界面上发生的，反射光发生半波损失而与入射光反相。

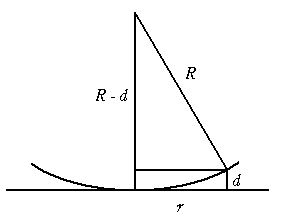
牛顿环因反射光或投射光而有所不同。公式如下：

平凸透镜和平面透镜之间的空间薄膜的距离：

${\displaystyle d=R-<!--\; -\; -->\sqrt{R^2-<!--\; -\; -->r^2}}$

当完全相长干涉发生时：

其中m为非负整数0，1，2，……，即第一光环、第二光环……

反射光的牛顿环的强度分布公式：${\displaystyle Ir=\sin <!--\; \; -->(\frac{2\mathrm{\pi <!--\; \pi \; -->}(R-<!--\; -\; -->\sqrt{R^2-<!--\; -\; -->r^2})}{\mathrm{\lambda <!--\; \lambda \; -->}}{)}^2}$

透射光的牛顿环强度分布公式：${\displaystyle It=\cos <!--\; \; -->(\frac{2\mathrm{\pi <!--\; \pi \; -->}(R-<!--\; -\; -->\sqrt{R^2-<!--\; -\; -->r^2})}{\mathrm{\lambda <!--\; \lambda \; -->}}{)}^2}$

反射光牛顿环中心${\displaystyle r=0}$，${\displaystyle Ir=0}$，即中心强度为零，看见黑班。

透射光牛顿环中心${\displaystyle r=1}$，${\displaystyle It=1}$，可见亮斑。

牛顿环的直径与透镜的半径成正比，透镜半径越大，环也越大。

牛顿环的直径与波长成正比，波长越长，环越大。即红色光的牛顿环大，蓝色光的牛顿环小。