卡诺图

✍ dations ◷ 2025-11-24 05:22:44 #数字电子,布尔代数,图表

卡诺图是真值表的变形，它可以将有n个变量的逻辑函数的 $2^{n}$ $2^{n}$ 个最小项组织在给定的长方形表格中，同时为相邻最小项（相邻与项）运用邻接律化简提供了直观的图形工具。但是，如果需要处理的逻辑函数的自变量较多（有五个或更多的时候，此时有些项就很难圈了），那么卡诺图的行列数将迅速增加，使图形更加复杂。:189

卡诺图是贝尔实验室的电信工程师，莫里斯·卡诺（Maurice Karnaugh）在1953年发明的。

接下来我们用两个不同的写法，及四个不同的布尔变量A, B, C, D和他们的相反值，来表示同一个尚未化简的布尔代数：

把函数包含的所有最小项，以“1”填入变量卡诺图对应编号的小格内。

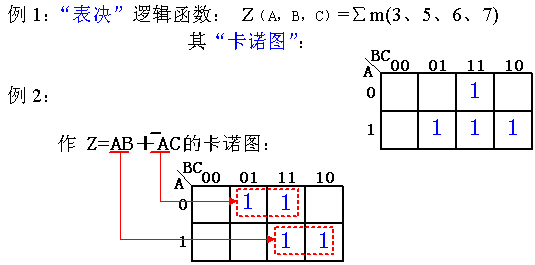
在进行化简时，如果用图中真值为0的项更方便，可以用他们来处理，方法和真值取1时一样，只是结果要再做一次求反。

相关

烷烃列表以下的列表示介绍常见正构烷烃的物理性质。高级烷烃
查德·米尔金查德·亚历山大·米尔金（英语：Chad Alexander Mirkin，1963年11月23日－），美国化学家，西北大学教授。1986年毕业于狄金森学院（理学士），1989年取得宾夕法尼亚州立大学的博士学位。
广电三法广电三法，是中华民国（台湾）的三项广播电视相关法律，包括《广播电视法》、《有线广播电视法》、《卫星广播电视法》。为了推动通讯汇流，最早自2002年起，陆续有多次修法。《广播电视
尼古拉斯·雷尼古拉斯·雷（Nicholas Ray，1911年8月7日－1979年6月16日）是一位美国知名电影导演，擅长于史诗电影与黑色幽默电影。
王滨 (1912年)王滨（1912年－1960年），原名王绍杰，又名王斌，男，山东昌邑人，中国导演、编剧、演员，中国电影家协会会员。
爱德万测试爱德万测试（英语：Advantest Corporation，全称：株式会社爱德万测试），日本的上市公司，成立于1954年7月1日。
灰胡椒鲷灰胡椒鲷（学名：）为石鲈科胡椒鲷属的鱼类。分布于台湾岛等。该物种的模式产地在红海。
同人小说同人小说（英语：Fan fiction），是同人作品的一类，指的是利用原有漫画、动画、小说、影视作品中的人物角色、故事情节或背景设定等元素进行的二次创作。由于同人小说的整体结构、人
周俊周俊可以指：
元维基元维基是维基媒体基金会旗下负责各维基媒体计划之间协调工作的项目，它是一个众多维基媒体的发送消息的中心。其中重要的帮助文件都首先在元维基上发布后再复制或翻译后应用到