半精度浮点数 是一种被计算机使用的二进制浮点数据类型。半精度浮点数使用2个字节(16位)来存储。
在IEEE 754-2008中,它被称作binary16。这种数据类型只适合存储对精度要求不高的数字,不适合用来计算。
半精度浮点数是一种较新的浮点类型。 英伟达在2002年初发布的Cg语言中称它作 half 类型,并首次在2002年末发布的GeForce FX中实现。ILM 当时正在寻找一种拥有高动态范围,且不需过多消耗硬盘和内存,并且能像单精度浮点数和双精度浮点数那样被用来进行浮点计算的图像格式。由SGI的John Airey领导的硬件加速可编程着色小组在1997年发明了作为'bali'设计工作的一部分的s10e5数据类型,曾在SIGGRAPH 2000年的论文中介绍过。(见章节 4.3)并且在美国专利7518615中被进一步记录。
半精度浮点数可在OpenEXR, JPEG XR, OpenGL, Cg语言、D3DX等计算机图形环境中使用。其与8位或16位整数相比具有动态范围高的优点,可以使高对比度图片中更多细节得以保留。与单精度浮点数相比,它的优点是只需要一半的存储空间和带宽(但是会牺牲精度和数值范围)。
IEEE 754 标准指定了一个 binary16 要有如下的格式:
按如下顺序排列:
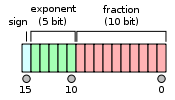
除非指数位全是0,否则就会假定隐藏的起始位是1。因此只有10位尾数在内存中被显示出来,而总精度是11位。据IEEE 754的说法,虽然尾数只有10位,但是尾数精度是11位的(log10(211) ≈ 3.311 十进制数).
0 01111 0000000000 = 10 01111 0000000001 = 1 + 2−10 = 1.0009765625 (1之后的最接近的数)1 10000 0000000000 = −20 11110 1111111111 = 65504 (max half precision)0 00001 0000000000 = 2−14 ≈ 6.10352 × 10−5 (最小正指数)0 00000 1111111111 = 2−14 - 2−24 ≈ 6.09756 × 10−5 (最大尾数)0 00000 0000000001 = 2−24 ≈ 5.96046 × 10−8 (最小正尾数)0 00000 0000000000 = 01 00000 0000000000 = −00 11111 0000000000 = infinity1 11111 0000000000 = −infinity0 01101 0101010101 = 0.333251953125 ≈ 1/3
由于尾数的位数是奇数,所以默认情况下,1/3 这类的数会像双精度浮点数一样四舍五入。
