锥状分布

在数学上，锥状分布（Cone-shaped distribution function）是科恩克莱斯分布系列函数中的一种。锥状分布于公元1991年由 Yunxin Zhao、Les E. Atlas 和 Robert J. Marks 提出。本分布之核心函数 ${\displaystyle \mathrm{\varphi <!--\; \varphi \; -->}\left(t,\mathrm{\tau <!--\; \tau \; -->}\right)}$ 于${\displaystyle t,\mathrm{\tau <!--\; \tau \; -->}}$ 域之分布形似锥状，故得名。

锥状分布的定义如下

其中

其核心函数 ${\displaystyle \mathrm{\Phi <!--\; \Phi \; -->}\left(\mathrm{\eta <!--\; \eta \; -->},\mathrm{\tau <!--\; \tau \; -->}\right)}$ 定义为

其中 ${\displaystyle \mathrm{\alpha <!--\; \alpha \; -->}}$ 为一可调整之参数。

由 ${\displaystyle \mathrm{\varphi <!--\; \varphi \; -->}\left(t,\mathrm{\tau <!--\; \tau \; -->}\right)={\mathcal{F}}^{-<!--\; -\; -->1}}$ 可得

下图为锥状分布之核心函数于 ${\displaystyle t,\mathrm{\tau <!--\; \tau \; -->}}$ 域之大小分布

下列图形为锥状分布之核心函数于 ${\displaystyle \mathrm{\eta <!--\; \eta \; -->},\mathrm{\tau <!--\; \tau \; -->}}$ 域不同 ${\displaystyle \mathrm{\alpha <!--\; \alpha \; -->}}$ 值时之大小分布

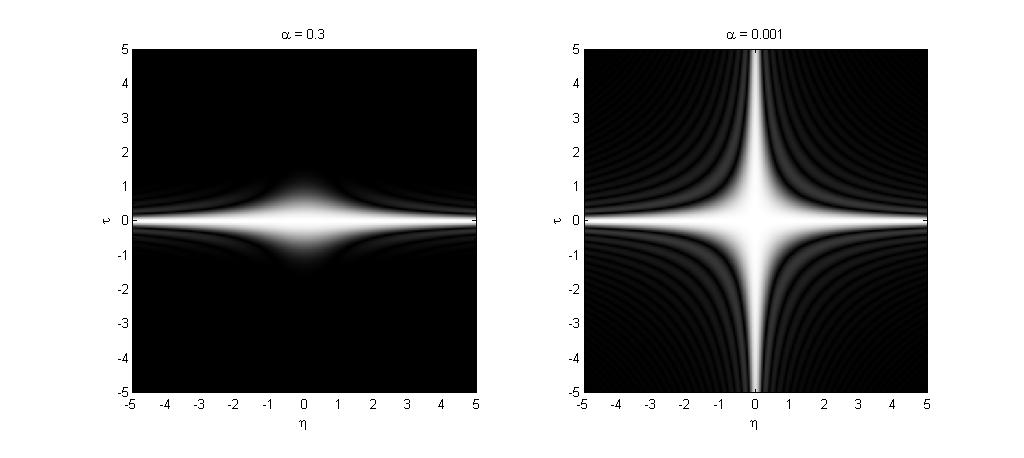
观察上图可知，我们可以透过选取适当的 ${\displaystyle \mathrm{\alpha <!--\; \alpha \; -->}}$ 值得到适合的 ${\displaystyle \mathrm{\Phi <!--\; \Phi \; -->}\left(\mathrm{\eta <!--\; \eta \; -->},\mathrm{\tau <!--\; \tau \; -->}\right)}$ 以滤除掉延 ${\displaystyle \mathrm{\tau <!--\; \tau \; -->}}$ 轴的噪声或干扰。

当输入信号由二具有相同或相近中心频率的成分组成，使用锥状分布作为核心函数可以完全滤除交叉项。相反地，本分布无法滤除当输入信号由二具有相同或相近中心时间的成分组成所形成之交叉项。