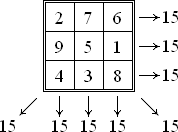
幻方常数或幻方和是指一个幻方中任一行、任一列或对角线的和。例如以下的三阶幻方的幻方常数是15。
“幻方常数”或“幻方和”一词也可以延伸到幻星或幻立方(英语:Magic cube)中。
若一n阶幻方是由1到n2的整数组成,则其幻方常数只和n有关,其数值为
以下是整数1到k的和
若要计算幻方中所有数字的和,令 k = n2,因此和为 n2(n2+1)/2,因为幻方共有n列,每列的和相同,和除以n就是幻方常数。
以下是n为3,4,5……时,由整数1到n2组成n阶幻方的幻方常数(OEIS中的数列A006003):
15, 34, 65, 111, 175, 260, 369, 505, 671, 870, …
一个由1到n3的整数组成的幻立方,其幻方常数如下所示(OEIS中的数列A027441):
在四维空间中,一个由1到n3的整数组成的幻超正方体,其幻方常数为
若一个d维n阶的幻超立方体,由一个由1到nd的整数组成,其幻方常数可表示为
若一个有n个角的幻星,由一个由1到2n的整数组成,其幻方常数可表示为
