枢纽定理

✍ dations ◷ 2025-12-07 11:53:19 #枢纽定理

枢纽定理是一个平面几何定理，是三角形的基本性质之一，通常会以两组三角形作比较。若有两组三角形，这两个三角形有两组对应边相等，则三角形的边所夹的角，角度愈大，则三角形的第三边也愈大。枢纽定理也有正定理和逆定理之分，正性质是由夹角的角度大小推出第三边的长短，而逆性质则是由第三边的长短来推出对角夹角角度大小。

枢纽的枢是指门在转动时的轴心，枢纽又叫“活页”或“后纽”；纽有脉络或系带的意思。类似一个事情的脉络或主轴的意思，这边借由其夹角转动来比喻以一个轴心固定两个边。

证明的方法不只一种，以下给出其中一种证明。如图，给出两个三角形，△ABC及△A'B'C'，边AB=边A'B'，边AC=边A'C'，∠A>∠A'。如图，将边AB与边A'B'重叠。

Triangle-shu-niu-A Triangle-shu-niu-B Triangle-shu-niu-C

作∠C'AC的角平分线，交边BC于D点，连接C'D。

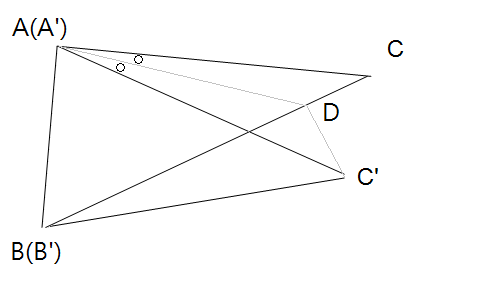
Triangle-shu-niu-D

∵边AD=边A'D

∠CAD=∠C'AD

边AC=边AC'

∴△ACD≅△AC'D (SAS全等性质)

故CD=C'D

又一三角形任两边之和大于第三边，边BD+边DC'>边BC'，则边BD+边DC>边BC'，故边BC>边B'C'。

相关

库安多古班哥省宽多-库邦戈省位于安哥拉东南端，与比耶省、库内纳省、威拉省、莫希科省等省份及纳米比亚、津巴布韦相邻。
微晶微晶（英语：microcrystal），也称微晶体，指的是只能在显微镜下看到的微小晶体。与之相对的是粗晶（macrocrystal），指的是肉眼可以很容易分辨的晶体。
大浪街道大浪街道是中国广东省深圳市龙华区下辖的一个街道，挨着龙华街道，与石岩街道、光明街道、观澜街道相邻，有机荷高速公路经过。大浪街道总面积37.2平方公里，常住总人口约30万人，其中
兰乔多明格兹兰乔多明格兹（英语：Rancho Dominguez）是位于美国加利福尼亚州洛杉矶县的一个非建制地区。该地的面积和人口皆未知。兰乔多明格兹的座标为33°53′23″N 118°16′07″W / 33.88
墨西哥电信Telmex，即墨西哥电信公司，总部位于墨西哥市，为墨西哥以及其他的如阿根廷、智利、哥伦比亚、巴西、厄瓜多尔、秘鲁、委内瑞拉等拉美国家提供的电信产品和服务。 Telmex仍然是
京都市交通局京都市交通局（日语：京都市交通局／きょうとしこうつうきょく */?）是经营京都府京都市内及附近地区公营交通事业的京都市的一家地方公营企业。主要运营地铁（京都市营地铁）、公车（
自由联合协定自由联合协定（英语：Compact of Free Association，简称COFA）是美国与三个太平洋岛国签署的国际协定，确立并制定了彼此间联系国的关系。这三个岛国与北马里亚纳群岛自由邦之前组成
刘吉典刘吉典（1919年－2014年8月24日－），作曲家，大学文化，著有《京剧音乐概论》、《刘吉典戏曲音乐作品选集》等书。他是中华人民共和国成立后参与京剧改革，影响较大的文化人，1955年中国京剧
猴面蟹科猴面蟹科（学名：Camptandriidae）是短尾下目沙蟹总科之下的一个科，其下包括有21个属38个物种。猴面蟹科旗下包括下列各个属：
雪白山雪白山（H2444m），又名泰矢生山；位于桃园市复兴区与新竹县尖石乡交界处，海拔2444.305米，为桃园市最高峰。立有一座编号1531二等三角点花冈基石，位于雪白营地上方。山顶处于树林间且无