Maple

✍ dations ◷ 2025-10-24 13:39:04 #数值分析软件,C软件,计算笔记本,Linux计算机代数系统软件,MacOS计算机代数系统软件,Windows计算机代数系统软件,跨平台软件,数据可视化软件,数据

MAPLE是一个符号运算和数值计算软件平台

用户能够直接使用传统数学符号进行输入，也可以定制个性化的界面。对于数值计算有额外的支持，能够扩展到任意精度，同时亦支持符号演算及可视化。符号演算的例子参见下文。Maple内建有一种动态的命令行风格的编程语言，该语言支持具有作用域的变量。同时亦有其他语言的接口（C、FORTRAN、Java、Matlab和Visual Basic）。还具有与Excel进行交互的接口。

Maple由一个很小的由C语言编写的内核提供Maple语言。许多功能由各种来源的函数库提供。许多数值计算由NAG数值计算库, ATLAS库, GNU多精度库提供。大部分库由Maple语言编写，并且可查看源代码。

Maple中不同的功能需要不同格式的数值数据。符号表达式在内存中以有向无环图的形式存储。标准界面和计算界面由Java语言编写。经典界面由C语言编写。

简单命令式程序的构造：

myfac := proc(n::nonnegint)   local out, i;   out := 1;   for i from 2 to n do       out := out * i   end do;   outend proc;

一些简单的函数也可以使用直观的箭头表示法表示

myfac := n -> product( i, i=1..n );

开方

evalf(2^1/12)

1.059463094359295264561825294946341700779204317494185628559208431458761646063255722383768376863945569

f:=x^2-63*x+99=0;

solve(f,x);

${\frac {63}{2}}+{\frac {3}{2}}*{\sqrt {(}}397)$ ${\frac {63}{2}}+{\frac {3}{2}}*{\sqrt (}397)$ , ${\frac {63}{2}}-{\frac {3}{2}}*{\sqrt {(}}397)$ ${\frac {63}{2}}-{\frac {3}{2}}*{\sqrt (}397)$

f := x^7+3*x = 7;

solve(f,x);

evalf(%);

f := sin(x)^3+5*cosh(x) = 0;

$sin^{3}(x)+5cosh(x)=0$ $sin^{3}(x)+5cosh(x)=0$

> solve(f, x);

RootOf( $sin^{3}(Z)-arccosh({\frac {-1}{5}}sin(Z)))$ $sin^{3}(Z)-arccosh({\frac {-1}{5}}sin(Z)))$

> evalf(%);

根据 $x-y>6$ $x-y>6$ ，寻找 $(x+y)^{5}=9$ $(x+y)^{5}=9$ 的所有整数解。

solve({x-y > 6, (x+y)^5 = 9}, );

答案： ${\displaystyle }$ $\text{[math]}$

计算矩阵的行列式。

M:= Matrix(], , ]);  # 矩阵样例

{\begin{bmatrix}1&2&3\\a&b&c\\x&y&z\end{bmatrix}}

{\begin{bmatrix}1&2&3\\a&b&c\\x&y&z\end{bmatrix}}

with(LinearAlgebra)

m:=Determinant(M);

答案： $bz-cy+3ay-2az+2xc-3xb$ $bz-cy+3ay-2az+2xc-3xb$

with(VectorCalculus);

w:=Wronskian(,x)

Matrix(3, 3, {(1, 1) = 1, (1, 2) = x, (1, 3) = x^3+x-1, (2, 1) = 0, (2, 2) = 1, (2, 3) = 3*x^2+1, (3, 1) = 0, (3, 2) = 0, (3, 3) = 6*x})

d:=Determinant(w);

J := Jacobian(, );

m:=Matrix(2, 2, {(1, 1) = cos(t), (1, 2) = -r*sin(t), (2, 1) = sinh(t), (2, 2) = r*cosh(t)})

d:=Determinant(m);

sin(t)*r^2*sinh(t)-2r^2cos(t)cosh(t)

f := x^3+y*cos(x)+t*tan(y))

with(VectorCalculus);

h:=hessian(f,);

${\begin{bmatrix}6*x-y*cos(x)&-sin(x)&0\\-sin(x)&2*t*tan(y)*(1+tan(y)^{2})&1+tan(y)^{2}\\0&1+tan(y)^{2}&0\end{bmatrix}}$ ${\begin{bmatrix}6*x-y*cos(x)&-sin(x)&0\\-sin(x)&2*t*tan(y)*(1+tan(y)^{2})&1+tan(y)^{2}\\0&1+tan(y)^{2}&0\end{bmatrix}}$

求 $\int \cos \left({\frac {x}{a}}\right)dx$ $\int \cos \left({\frac {x}{a}}\right)dx$ .

int(cos(x/a), x);

答案： $a\sin \left({\frac {x}{a}}\right)$ $a\sin \left({\frac {x}{a}}\right)$

求 $\int \sin \left({\frac {x}{a}}\right)dx$ $\int \sin \left({\frac {x}{a}}\right)dx$ .

int(sin(x/a), x);

答案： $-a\cos \left({\frac {x}{a}}\right)$ $-a\cos \left({\frac {x}{a}}\right)$

注意：Maple在积分时不提供常数项C，必须自行补上。

> int(cos(x/a), x = 1 .. 5);

计算以下线性常微分方程的一个精确解 ${\frac {d^{2}y}{dx^{2}}}(x)-3y(x)=x$ ${\frac {d^{2}y}{dx^{2}}}(x)-3y(x)=x$ 初始条件为 $y(0)=0,\quad \left.{\frac {dy}{dx}}\right|_{x=0}=2$ $y(0)=0,\quad \left.{\frac {dy}{dx}}\right|_{{x=0}}=2$

dsolve( {diff(y(x),x,x) - 3*y(x) = x, y(0)=0, D(y)(0)=2}, y(x) );

答案： $y(x)={\frac {7}{18}}{\sqrt {3}}e^{{\sqrt {3}}x}-{\frac {7}{18}}{\sqrt {3}}e^{-{\sqrt {3}}x}-{\frac {1}{3}}x$ $y(x)={\frac {7}{18}}{\sqrt {3}}e^{{{\sqrt {3}}x}}-{\frac {7}{18}}{\sqrt {3}}e^{{-{\sqrt {3}}x}}-{\frac {1}{3}}x$

dsolve(diff(y(x), x, x) = x^2*y(x))

解：

+ $C_{2}{\sqrt {(}}x)$ $C_{{2}}{\sqrt (}x)$ BesselK( $1 \over 4$ ${1 \over 4}$ , $1 \over 2$ ${1 \over 2}$ $x^{2}$ $x^{2}$ )

series(tanh(x),x=0,15)

x-{\frac {1}{3}}\,x^{3}+{\frac {2}{15}}\,x^{5}-{\frac {17}{315}}\,x^{7}

x-{\frac {1}{3}}\,x^{3}+{\frac {2}{15}}\,x^{5}-{\frac {17}{315}}\,x^{7}

+{\frac {62}{2835}}\,x^{9}-{\frac {1382}{155925}}\,x^{11}+{\frac {21844}{6081075}}\,x^{13}+{\mathcal {O}}(x^{15})

+{\frac {62}{2835}}\,x^{9}-{\frac {1382}{155925}}\,x^{11}+{\frac {21844}{6081075}}\,x^{13}+{\mathcal {O}}(x^{15})

f:=int(exp^cosh(x),x)series(f,x=0,15);

ex+{\frac {1}{6}}ex^{3}+{\frac {1}{30}}ex^{5}+{\frac {31}{5040}}ex^{7}+{\frac {379}{362880}}ex^{9}

ex+{\frac {1}{6}}ex^{3}+{\frac {1}{30}}ex^{5}+{\frac {31}{5040}}ex^{7}+{\frac {379}{362880}}ex^{9}

+{\frac {149}{907200}}ex^{11}+{\frac {150349}{6227020800}}ex^{13}+{\frac {4373461}{1307674368000}}ex^{15}+{\mathcal {O}}(x^{17})

+{\frac {149}{907200}}ex^{11}+{\frac {150349}{6227020800}}ex^{13}+{\frac {4373461}{1307674368000}}ex^{15}+{\mathcal {O}}(x^{17})

拉普拉斯变换

with(inttrans);

> f := (1+A*t+B*t^2)*exp(c*t);

$(1+A*t+B*t^{2})*e^{c*t}$ $(1+A*t+B*t^{2})*e^{{c*t}}$

> laplace(f, t, s);

${\frac {1}{s-c}}+{\frac {A}{(s-c)^{2}}}+{\frac {2B}{(s-c)^{3}}}$ ${\frac {1}{s-c}}+{\frac {A}{(s-c)^{2}}}+{\frac {2B}{(s-c)^{3}}}$

invlaplace(1/(s-a),s,x)

$e^{ax}$ $e^{{ax}}$

z := y(t);

${\frac {d^{2}}{dt^{2}}}y(t)+a{\frac {d}{dt}}y(t)=by(t)$ ${\frac {d^{2}}{dt^{2}}}y(t)+a{\frac {d}{dt}}y(t)=by(t)$

with(inttrans);

${\frac {d^{2}}{dt^{2}}}y(t)+a{\frac {d}{dt}}y(t)=by(t)$ ${\frac {d^{2}}{dt^{2}}}y(t)+a{\frac {d}{dt}}y(t)=by(t)$

with(inttrans);

fourier(sin(x),x,w)

$\Pi$ $\Pi$ *(Dirac(w-1)+Dirac(w+1))

绘制函数 $y=x\cdot \sin x$ $y=x\cdot \sin x$ ， $x\in (-10,10)$ $x\in (-10,10)$

plot(x*sin(x),x=-10..10);

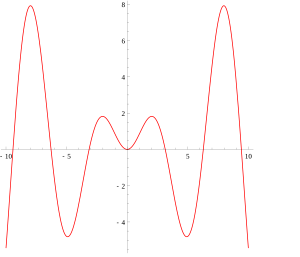
绘制函数 $x^{2}+y^{2}$ $x^{2}+y^{2}$ ， $x {\displaystyle x}$ $x$ 和 $y {\displaystyle y}$ $y$ 的范围为 -1到1

plot3d(x^2+y^2,x=-1..1,y=-1..1);

$f:=2*k^{2}/cosh(k*(x-4*k^{2}*t))^{2}$ $f:=2*k^{2}/cosh(k*(x-4*k^{2}*t))^{2}$

with(plots);

animate(subs(k = .5, f), x = -30 .. 30, t = -10 .. 10, numpoints = 200, frames = 50, color = red, thickness = 3);

with(plots)

animate3d(cos(t*x)*sin(3*t*y), x = -Pi .. Pi, y = -Pi .. Pi, t = 1 .. 2)

求解偏微分方程组

条件为 $v(x,t)\neq 0$ $v(x,t)\neq 0$ .

eqn1:= diff(v(x, t), x) = -u(x,t)*v(x,t):eqn2:= diff(v(x, t), t) = -v(x,t)*(diff(u(x,t), x))+v(x,t)*u(x,t)^2:eqn3:= diff(u(x,t), t)+2*u(x,t)*(diff(u(x,t), x))-(diff(diff(u(x,t), x), x)) = 0:pdsolve({eqn1,eqn2,eqn3,v(x,t)<>0},): op(%);

答案： $v\left(x,t\right)={e^{{\sqrt {{\it {\_c}}_{1}}}x}}{\it {\_C3}}\,{e^{{\it {\_c}}_{1}t}}{\it {\_C1}}+{\frac {{\it {\_C3}}\,{e^{{\it {\_c}}_{1}t}}{\it {\_C2}}}{e^{{\sqrt {{\it {\_c}}_{1}}}x}}},\ \ u\left(x,t\right)=-{\frac {{\sqrt {{\it {\_c}}_{1}}}\left({\it {\_C1}}\,\left({e^{{\sqrt {{\it {\_c}}_{1}}}x}}\right)^{2}-{\it {\_C2}}\right)}{{\it {\_C1}}\,\left({e^{{\sqrt {{\it {\_c}}_{1}}}x}}\right)^{2}+{\it {\_C2}}}}$ $v\left(x,t\right)={e^{{{\sqrt {{{\it {\_c}}}_{{{1}}}}}x}}}{{\it {\_C3}}}\,{e^{{{{\it {\_c}}}_{{{1}}}t}}}{{\it {\_C1}}}+{{\frac {{{\it {\_C3}}}\,{e^{{{{\it {\_c}}}_{{{1}}}t}}}{{\it {\_C2}}}}{{e^{{{\sqrt {{{\it {\_c}}}_{{{1}}}}}x}}}}}},\ \ u\left(x,t\right)=-{{\frac {{\sqrt {{{\it {\_c}}}_{{{1}}}}}\left({{\it {\_C1}}}\,\left({e^{{{\sqrt {{{\it {\_c}}}_{{{1}}}}}x}}}\right)^{{2}}-{{\it {\_C2}}}\right)}{{{\it {\_C1}}}\,\left({e^{{{\sqrt {{{\it {\_c}}}_{{{1}}}}}x}}}\right)^{{2}}+{{\it {\_C2}}}}}}$

寻找函数 $f {\displaystyle f}$ $f$ 满足积分方程 $f(x)-3\int _{-1}^{1}(xy+x^{2}y^{2})f(y)dy=h(x)$ $f(x)-3\int _{{-1}}^{1}(xy+x^{2}y^{2})f(y)dy=h(x)$ .

eqn:= f(x)-3*Integrate((x*y+x^2*y^2)*f(y), y=-1..1) = h(x):intsolve(eqn,f(x));

答案： $f\left(x\right)=\int _{-1}^{1}\!\left(-15\,{x}^{2}{y}^{2}-3\,xy\right)h\left(y\right){dy}+h\left(x\right)$

Maple

开方

拉普拉斯变换

相关