时频分析

✍ dations ◷ 2024-09-20 08:49:59 #信号处理,时频分析

时频分布是一项让我们能够同时观察一个讯号的时域和频域资讯的工具，而时频分析就是在分析时频分布。传统上，我们常用傅里叶变换来观察一个讯号的频谱。然而，这样的方法不适合用来分析一个频率会随着时间而改变的讯号，由于傅里叶变换只分析了一维的讯号分布，而时频分析却能分析二维(时域跟频域)的讯号分布，因此在讯号处理中更常被运用。

时频分析也可以说是傅里叶分析的一般化，通常用于频率特性会随时间而变化的讯号上，而在日常生活中符合符合此特性的讯号非常多，像是演讲、音乐、影像、医学讯号...等，因此能应用的领域相当广泛。

另外，更实际应用时频分析的动机为传统傅里叶分析假设讯号在时域是无限长或是周期性出现的，然而在现实中许多讯号都只有短暂的存在，而且在讯号持续期间可能有相当大的变化。举例来说，传统的音乐乐器不会持续产生无限长的正弦波，反而可能突然有一巨声，然后渐渐减弱。因此时频分析的研究势不可挡。

让我们看看以下这个频率会随时间变化的讯号例子：

$x(t)={\begin{cases}\cos(\pi t);&t<10\\\cos(3\pi t);&10\leq t<20\\\cos(2\pi t);&t>20\end{cases}}$ $x(t)={\begin{cases}\cos(\pi t);&t<10\\\cos(3\pi t);&10\leq t<20\\\cos(2\pi t);&t>20\end{cases}}$

一旦这样的数学式成立，便可利用时频分析的各种技术，萃取讯号中的各种有用资讯，并分离噪音或干扰。

最早的时频分析方法应见于Alfréd Haar提出的哈尔小波转换(1909)，然而在当时因时频分析所需的运算量仍是个无法忽视的议题，因此并未广泛应用于讯号处理。而后更多的贡献来自于Dennis Gabor，像是小波前身Gabor atoms (1947)，以及加伯转换和改进型的短时距傅里叶变换。维格纳准几率分布(Ville 1948)也是一个重要的开端。

特别在1930年代及1940年代，早期的时频分析方法恰好与量子力学的发展一致，这反映了位置-动量平面及时域-频域平面的数学机制有些共通性，像是海森堡不确定性原理(量子力学)与加伯限制(时频分析)最终都得出了扭对称几何结构。

常见的时频分布函数有短时距傅里叶变换（包含加伯转换）、科恩分布函数（包含韦格纳分布）、改进型韦格纳分布，以及加伯-韦格纳分布（Gabor-Wigner distribution function）函数及S转换等。

而这些看似不同的时频分析函数，其数学公式的由来都有些相关性，若想对时频分析的了解更加透彻，应在学习时将它们一起理解，而非都视为单一函数，像是做1/4次傅里叶变换可以解读成傅里叶变换在时频分析平面上转90°，而这个旋转做了4次后就会回到原本的函数，只做2次时则会视反转的图形。

一个理想的时频分布函数有助于我们做时频分析，而它大致上具有以下四种性质：

在这里我们比较几个较常用的时频分析之优劣度。

为了能顺利的分析各讯号之时频分布，选择适当的时频分布函数是很重要的。而至于要如何选择时频分布函数呢？这端看于我们所要应用它的地方在哪边。韦格纳分布之定义中的自相关函数是一把双面刃，它让韦格纳分布函数拥有高的清晰度，然而，它也同时让它产生了cross-term的问题。

因此，如果我们想要分析一个只有单一项的讯号，此时不会有cross-term的产生，因此我们通常选择韦格纳分布函数来获得高清晰度；另一方面，如果我们要分析的讯号是由很多个项所组成的，此时若用韦格纳分布会有cross-term产生，所以我们可能选择用加伯转换或是加伯-韦格纳分布函数会比较好。

在接下来即将介绍的应用中，我们除了需要时频分布函数，还需要搭配其他的运算才能达到目的，而著名的线性标准转换（Linear canonical transform）可以帮助我们。我们可以利用线性标准转换来任意的改变一个讯号在时频分布平面上面的形状和位置，像是水平以及垂直的移动、扩大、shearing（扭曲），以及旋转（用分数傅里叶变换，fractional Fourier transform, FRFT）等。由此可见，线性标准转换让我们对于时频分布的处理更灵活。

这边我们列举一些时频分布之应用的例子。

瞬间频率的定义是 ${\frac {1}{2\pi }}{\frac {d}{dt}}\phi (t)$ ${\frac {1}{2\pi }}{\frac {d}{dt}}\phi (t)$ ，其中 $\phi (t)$ $\phi (t)$ 是讯号的瞬时相位。我们可以直接由时频分布的图形中看出每个时刻的瞬时频率是多少，不过前提是这个时频分布的图形要够清晰，因此，我们经常选用韦格纳分布函数来做进一步的分析。

滤波器的目的就是要移除我们不要的部分，并保留我们要的部分。在没有应用时频分布之前，我们只能分别在时域跟频域上面来做过滤的动作，如下所示。
Filter tf.jpg
像上面这样只能分别在时域或频域上过滤的方式，并不适合处理每一种讯号。如果讯号在时域上或在频域上有重叠的话，这时候使用时频分布函数来做分析过滤，并搭配线性完整转换的操作，就可以做出更有效且灵活的滤波器。让我们看看以下的例子。
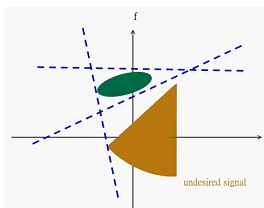
$Filter fractional.jpg$
而在滤波器设计的应用中，时频分布通常处理的讯号是由很多个项所组成的，因此若用韦格纳分布来做分析的话，将会产生cross-term的问题。或许加伯转换、加伯-韦格纳分布函数，亦或Cohen's class 分布函数会是比较好的选择。

讯号分解的概念就跟滤波器设计很类似。

由 Nyquist-Shannon取样定理且经过一番推导，我们大致上可以说一个讯号经过取样后而不产生失真（aliasing）的最低取样点数，会和这讯号在时频平面上图形的面积相等（事实上，没有一个讯号在时频平面上的面积有限的，因此我们省略了一些精确度）。接下来，让我们看看传统取样定理跟结合了时频分析以后的取样定理之差异。

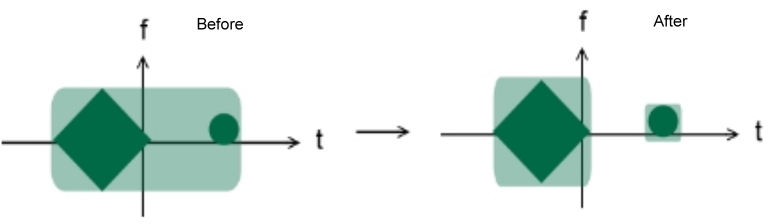
若浅绿色的部分是我们取样的涵盖范围，则我们可以很明显的看出使用时频分析后，所需取样的点数会比之前少了许多，因此加快了我们的运算。当我们使用韦格纳分布函数时，可能会产生cross-term；另一方面，若使用加伯转换做分析的话，又可能会因为清晰度不佳而让所需要取样的面积又变大了。因此，选用哪个函数要视讯号的情形而定，如果讯号是单一项组成的，那么就使用韦格纳分布函数；然而，如果讯号是由多项组成的，则用加伯转换、加伯-韦格纳分布函数，或是Cohen's class 分布函数。

取样点数(sampling points) = 时频分析面积的总和 + 其余额外参数

Step 1. 解析讯号转换

转换讯号到座标轴的同一边(一般是取该讯号的实数区)

$x(t)\rightarrow {\begin{alignedat}{2}x_{a}(t)&=x(t)+jx_{H}(t)\\x_{a}(f)&=x(f)+jH(f)x(f)\\\end{alignedat}},\ x_{H}(t):{\text{Hilbert transform of }}x(t)$ $x(t)\rightarrow {\begin{alignedat}{2}x_{a}(t)&=x(t)+jx_{H}(t)\\x_{a}(f)&=x(f)+jH(f)x(f)\\\end{alignedat}},\ x_{H}(t):{\text{Hilbert transform of }}x(t)$

$H(f)={\begin{cases}-j,&{\text{for }}f>0\\j,&{\text{for }}f<0\end{cases}},x_{a}(f)={\begin{cases}2x(f),&{\text{for }}f>0\\0,&{\text{for }}f<0\end{cases}}$ $H(f)={\begin{cases}-j,&{\text{for }}f>0\\j,&{\text{for }}f<0\end{cases}},x_{a}(f)={\begin{cases}2x(f),&{\text{for }}f>0\\0,&{\text{for }}f<0\end{cases}}$

Step 2. 讯号拆解

使用短时距傅里叶变换(short time Fourier transform, STFT; 因为讯号包含许多不同成分)来拆解讯号成许多部分。

Step 3. 使用斜推(shearing)或旋转(rotation)使各个部分减少到最小"面积"

使用韦格纳分布方程(Wigner distribution function, WDF; 因为此时讯号为单一成分且属随机程序)来斜推和翻转各个部分。

Step 4. 使用传统采样理论采样各个成分

$x_{d}=x(n\vartriangle _{t}),\vartriangle _{t}<1/F$ $x_{d}=x(n\vartriangle _{t}),\vartriangle _{t}<1/F$

$x(t)=\sum _{n}x_{d}sinc({\frac {t}{\vartriangle _{t}}}-n)$ $x(t)=\sum _{n}x_{d}sinc({\frac {t}{\vartriangle _{t}}}-n)$

严格来说，没有任何一个讯号的时频分布"面积"是有限的，但是我们可以选择一个阈值"threshold" Δ，使时频分析 $\left\vert X(t,f)\right\vert >\bigtriangleup$ $\left\vert X(t,f)\right\vert >\bigtriangleup$ 或是分布的面积是有限的。但若以"面积"来讨论取样点数，也会牺牲一些精确度。

如果 $x(t)$ $x(t)$ 是时间上有限的 $(x(t)=0{\text{ for }}t<t_{1}{\text{ and }}t>t_{2})$ $(x(t)=0{\text{ for }}t<t_{1}{\text{ and }}t>t_{2})$ , 则频率上则不可能是有限的。

如果 $x(t)$ $x(t)$ 是频率上有限的 $(X(f)=0{\text{ for }}f<f_{1}{\text{ and }}f>f_{2})$ $(X(f)=0{\text{ for }}f<f_{1}{\text{ and }}f>f_{2})$ ,则时间上则不可能是有限的。

只取 $t\in$ $t\in$ 和 $f\in$ $f\in$ 牺牲的能量所占的比例， $err={\frac {\int _{-\infty }^{t_{1}}|x(t)|^{2}dt+\int _{t_{2}}^{\infty }|x(t)|^{2}dt+\int _{-\infty }^{f_{1}}|X_{1}(f)|^{2}df+\int _{f_{2}}^{\infty }|X_{1}(f)|^{2}df}{\int _{-\infty }^{\infty }|x(t)|^{2}dt}}$ $err={\frac {\int _{-\infty }^{t_{1}}|x(t)|^{2}dt+\int _{t_{2}}^{\infty }|x(t)|^{2}dt+\int _{-\infty }^{f_{1}}|X_{1}(f)|^{2}df+\int _{f_{2}}^{\infty }|X_{1}(f)|^{2}df}{\int _{-\infty }^{\infty }|x(t)|^{2}dt}}$

$X_{1}(f)=FT,x_{1}(t)=x(t){\text{ for }}t\in ,x_{1}(t)=0{\text{ otherwise }}$ $X_{1}(f)=FT,x_{1}(t)=x(t){\text{ for }}t\in ,x_{1}(t)=0{\text{ otherwise }}$

$|x(t)|^{2}=\int _{-\infty }^{\infty }W_{x}(t,f)df,|X(f)|^{2}=\int _{-\infty }^{\infty }W_{x}(t,f)dt$ $|x(t)|^{2}=\int _{-\infty }^{\infty }W_{x}(t,f)df,|X(f)|^{2}=\int _{-\infty }^{\infty }W_{x}(t,f)dt$

$\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }W_{x}(t,f)dfdt=\int _{-\infty }^{\infty }|x(t)|^{2}dt={\text{ energy of }}x(t)$ $\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }W_{x}(t,f)dfdt=\int _{-\infty }^{\infty }|x(t)|^{2}dt={\text{ energy of }}x(t)$

${\begin{aligned}&\int _{-\infty }^{t_{1}}|x(t)|^{2}dt+\int _{t_{2}}^{\infty }|x(t)|^{2}dt+\int _{-\infty }^{f_{1}}|X_{1}(f)|^{2}df+\int _{f_{2}}^{\infty }|X_{1}(f)|^{2}df\\&=\int _{-\infty }^{t_{1}}\int _{-\infty }^{\infty }W_{x}(t,f)dfdt+\int _{t_{2}}^{\infty }\int _{-\infty }^{\infty }W_{x}(t,f)dfdt+\int _{-\infty }^{\infty }\int _{-\infty }^{f_{1}}W_{x_{1}}(t,f)dfdt+\int _{-\infty }^{\infty }\int _{f_{2}}^{\infty }W_{x_{1}}(t,f)dfdt\\&=\int _{-\infty }^{t_{1}}\int _{-\infty }^{\infty }W_{x}(t,f)dfdt+\int _{t_{2}}^{\infty }\int _{-\infty }^{\infty }W_{x}(t,f)dfdt+\int _{t_{1}}^{t_{2}}\int _{-\infty }^{f_{1}}W_{x_{1}}(t,f)dfdt+\int _{t_{1}}^{t_{2}}\int _{f_{2}}^{\infty }W_{x_{1}}(t,f)dfdt\\&\cong \int _{-\infty }^{t_{1}}\int _{-\infty }^{\infty }W_{x}(t,f)dfdt{\text{ (A) }}+\int _{t_{2}}^{\infty }\int _{-\infty }^{\infty }W_{x}(t,f)dfdt{\text{ (B) }}+\int _{t_{1}}^{t_{2}}\int _{-\infty }^{f_{1}}W_{x}(t,f)dfdt{\text{ (C) }}+\int _{t_{1}}^{t_{2}}\int _{f_{2}}^{\infty }W_{x}(t,f)dfdt{\text{ (D) }}\end{aligned}}$