折纸公理,又称藤田-羽鸟公理或藤田-贾斯汀公理,是折纸数学的基本公理。假定所有折纸操作均在理想的平面上进行,并且所有折痕都是直线,那么这些公理描述了通过折纸可能达成的所有数学操作。
折纸定理最早于1989年由雅克·贾斯汀(Jacques Justin)发现。截至目前为止,共推衍了6个公理,其中,公理1-6又于1991年由日裔意大利数学家藤田文章发现。定理7也于2001年由羽鸟公士郎发现。贾斯汀和罗伯特·朗(Robert J. Lang)也同样发现了公理7。
前6个公理又叫做藤田公理,公理7由羽鸟公士郎发现,贾斯汀和罗伯特·朗(Robert J. Lang)也同样发现了公理7。7条公理如下:
公理5可能有最多2个解,公理6可能有最多3个解,而尺规作图的公理最多只有两个解。所以,折纸的作图能力要强于尺规作图。就是说,尺规作图相当于在解二次方程,而折纸几何相当于解三次方程。因而诸如三等分角、倍立方等尺规作图无法解决的问题却可以用折纸几何解决。但是公理6在实践中需要将纸“滑动”,这其实相当于二刻尺作图,这在标准的尺规作图中是不被允许的。
罗伯特·朗证明了这七个公理已经是折纸几何的全部公理了。
给定两点 和 ,有且仅有一条折痕同时过这两点。
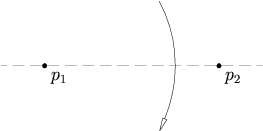
以参数方程表示的话,过2点的直线可以表示为:
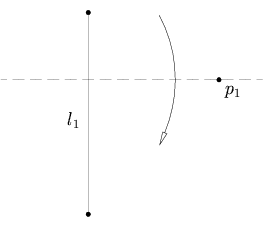
给定两点 和 ,有且仅有一种方法把 折到 上。

这条公理相当于是作线段 的垂直平分线。这可以通过以下四个步骤完成:
给定两直线 和 ,可以把 折到 上。

这条公理相当于是找出 和 组成的角的平分线。假设 和 是 上任意两点, 和 是 上任意两点, 和 分别是 和 方向的单位向量:
如果两直线不平行,它们的交点为:
其中
两条直线所夹的一个角的平分线方向是:
折痕的参数方程是:
这两直线还有另一个角平分线,两条角平分线互相垂直,且都过点 。而沿着任意一条角平分线折都能将 折到 上。但在实践中可能因为交点的位置(比如交点在纸外)使沿着其中一条角平分线的折叠无法实施。
如果两条直线平行,那么只要沿着两直线中间的一条线(与两直线平行,到两直线距离相等)折叠就可以将 折到 上
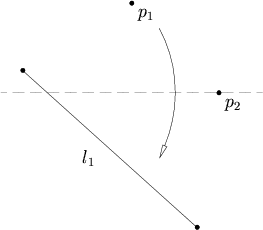
给定一点 和一条直线 ,有且仅有一种方法过 折出 的垂线。
向量 是垂直于 的单位向量,那么折痕的参数方程是:
给定两点 和 和一条直线 ,可以沿过 的直线将 折到 上。
这个公理相当于找出圆和直线的交点,所以有最多2个解,最少也可能无解。这取决于直线 和以 为圆心, 到 的距离为半径的圆的位置关系。如果直线和圆不相交则无解,相切则有1解,相交则有2解.
如果我们知道直线上两点 和 ,那么直线可以表示为:
如果圆心 ,半径 。那么这个圆可以表示为:
为了确定圆和直线的交点,将直线方程代入圆方程,得:
或者可以简化为:
其中:
然后,只要解以下方程就能确定直线和圆的交点:
如果判别式 ,那么方程无实数解,圆和直线没有交点;如果辨别式等于0,那么方程有一解,圆和直线相切;如果辨别式大于0,方程有两解,圆和直线有两个交点。令 和 是两个交点(如果存在),那么,我们可以得到线段如下:
折痕 垂直平分 ,可以将 折到 。同样,折痕 垂直平分 ,可以将 折到 。只要应用公理2就可以找到垂直平分线。折痕的参数方程是:
给定两点 和 和两直线 和 ,可以一次将 、 分别折到 、 上。
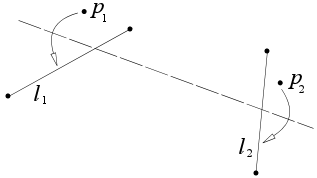
这个公理相当于找到同时与两条抛物线相切的直线,等价于解一个三次方程。两条抛物线的焦点分别是 和 ,准线分别是 和 。
给定一点 和两直线 和 ,可以沿着 的垂线将 折到 上。
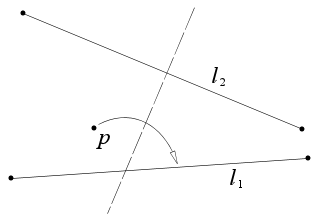
过 点作 的平行线,交 于 ,这个公理就是要找出线段 的垂直平分线。沿着这条垂直平分线折,就可以将 折到 上。
 和
和  ,有且仅有一条折痕同时过这两点。
,有且仅有一条折痕同时过这两点。 的垂直平分线。这可以通过以下四个步骤完成:
的垂直平分线。这可以通过以下四个步骤完成: 和
和  ,可以把
,可以把  和
和  是
是  和
和  分别是
分别是  。而沿着任意一条角平分线折都能将
。而沿着任意一条角平分线折都能将  和
和  ,那么直线可以表示为:
,那么直线可以表示为: ,半径
,半径  。那么这个圆可以表示为:
。那么这个圆可以表示为: ,那么方程无实数解,圆和直线没有交点;如果辨别式等于0,那么方程有一解,圆和直线相切;如果辨别式大于0,方程有两解,圆和直线有两个交点。令
,那么方程无实数解,圆和直线没有交点;如果辨别式等于0,那么方程有一解,圆和直线相切;如果辨别式大于0,方程有两解,圆和直线有两个交点。令 和
和  是两个交点(如果存在),那么,我们可以得到线段如下:
是两个交点(如果存在),那么,我们可以得到线段如下: 垂直平分
垂直平分  ,可以将
,可以将  垂直平分
垂直平分  ,可以将
,可以将  和两直线
和两直线  ,这个公理就是要找出线段
,这个公理就是要找出线段  的垂直平分线。沿着这条垂直平分线折,就可以将
的垂直平分线。沿着这条垂直平分线折,就可以将 